Приложения 

Ботвинников А.Д. § 10 [1]

Куб

  Ромбокубоктаэдр

pdf  Прочитай чертёж

pdf  Кто автор?

pdf  Что означают слова

pdf  Видео "1D-2D-3D-4D - Что это такое?"

pdf  Лента Мёбиуса

pdf 

Многообразие геометрических форм

На уроках математики вы уже познакомились с некоторыми геометрическими фигурами. Под фигурой понимают любую совокупность (множество) точек. Всякую сложную фигуру можно разделить на более простые.

Если все точки фигуры лежат в одной плоскости, фигуру называют плоской: треугольник, квадрат и др. Совокупность точек, расположенных в пространстве, образует пространственную фигуру: куб, цилиндр и др. Фигуры в пространстве называют  геометрическими телами.

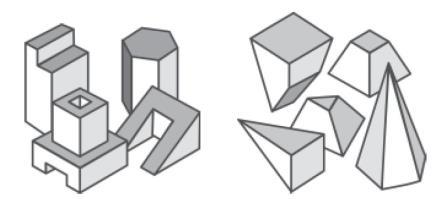
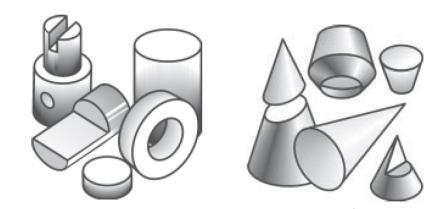
Предметы, которые нас окружают, детали машин имеют, как правило, сложную реальную геометрическую форму. Однако, присмотревшись к ним внимательно, можно заметить, что некоторые из них состоят из одного или нескольких простых геометрических тел или их видоизмененных частей. Такими геометрическими телами, образующими форму предметов, являются  призмы, пирамиды, цилиндры, конусы, шары и др. (рис. 1)

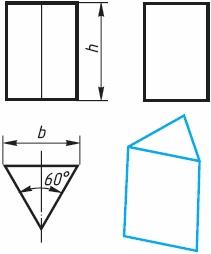
Рис. 1.  Геометрические тела

По форме простые геометрические тела делятся на многогранники и тела вращения. Плоскость является частным случаем поверхности.

Многогранники – геометрические тела, поверхность которых состоит из плоских многоугольников. Это куб, призма, параллелепипед, пирамида и др.

Тела вращения – геометрические тела, поверхность которых описывается какой-либо прямой или кривой (образующей) при её вращении вокруг неподвижной оси (например, конус, цилиндр, шар и т. п.).

Форма каждого геометрического тела имеет свои характерные признаки. По ним мы отличаем призму от цилиндра, пирамиду от конуса и  т. п. Эти признаки используются и при построении чертежей геометрических тел или состоящих из них предметов и деталей. Однако прежде чем выполнять такие чертежи, выясним, какие правила положены в основу способов их построения.

Поскольку форма большинства предметов представляет собой сочетание различных геометрических тел или их частей, для построения чертежей этих предметов необходимо знать, как изображается каждое геометрическое тело. Поэтому рассмотрим сначала построение чертежей и аксонометрических проекций простых тел. Это тем более необходимо, так как в сложной форме любого предмета всегда можно выделить простые геометрические тела, которые помогают представить форму предмета по его чертежу.

Изображение многогранников

Рассмотрим построение прямоугольных проекций призмы. Для примера возьмем треугольную призму (рис. 2) и шестиугольную призму (рис. 3). Их основания, параллельные горизонтальной плоскости проекций, изображаются на ней в натуральную величину, а на фронтальной и профильной плоскостях - отрезками прямых. Боковые грани изображаются без искажения на тех плоскостях проекций, которым они параллельны, и в виде отрезков прямых - на тех, которым перпендикулярны. Грани, наклонные к плоскостям, изображаются на них искаженными.

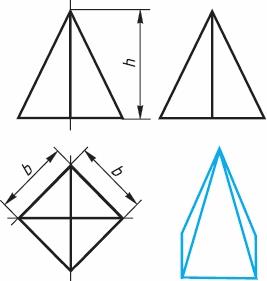
Рис. 2. Треугольная призма

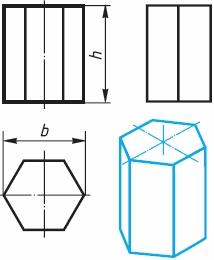
Рис. 3. Шестиугольная призма.

Размеры призм определяются их высотами и размерами фигур основания. Штрихпунктирными линиями на чертеже изображаются оси симметрии.

Рассмотрим, как изображают на чертеже правильную четырехугольную пирамиду (рис. 4). Основание пирамиды проецируется на горизонтальную плоскость проекций в натуральную величину. На нём диагоналями изображаются проекции боковых ребер, идущих от вершин основания к вершине пирамиды.

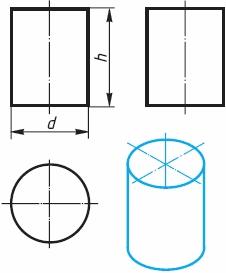
Рис. 4. Четырехугольная пирамида

Фронтальная и профильная проекции пирамиды - равнобедренные треугольники. Размеры пирамиды определяются длиной b двух сторон ее основания и высотой h.

Изображение тел вращения

Если круги, лежащие в основаниях цилиндра (рис. 5) и конуса 6), расположены параллельно горизонтальной плоскости проекций, их проекции на эту плоскость будут также кругами.

Рис. 5. Цилиндр

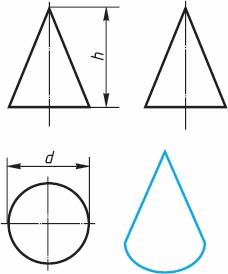
Рис. 6. Конус

Фронтальная и профильная проекции цилиндра в данном случае – прямоугольники, а конуса – равнобедренные треугольники.

На всех проекциях следует наносить оси симметрии, с проведения которых и начинают выполнение чертежей цилиндра и конуса.

Фронтальная и профильная проекции цилиндра одинаковы. То же можно сказать о проекциях конуса. Поэтому в данном случае профильные проекции на чертеже лишние. Кроме того, благодаря знаку диаметра Ø можно представить форму цилиндра и конуса даже по одной проекции (рис. 7, a и б). Отсюда следует, что в подобных случаях нет необходимости в трех проекциях. Размеры цилиндра и конуса определяются их высотой h и диаметром основания d.

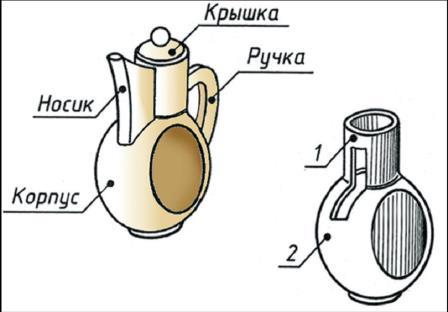
Рис. 7. Чертежи цилиндра, конуса и шара

Все проекции шара – круги, диаметр которых равен диаметру шара. На каждой проекции проводят центровые линии.

Благодаря знаку Ø, шар можно изображать в одной проекции (рис. 7, в). Но если по чертежу трудно отличить сферу от других поверхностей, то на чертеже добавляют слово «сфера», например: «Сфера Ø40».

Анализ геометрической формы

Вы знаете, что форма большинства предметов представляет собой сочетание различных геометрических тел или их частей. Следовательно, для чтения и выполнения чертежей нужно знать, как они изображаются.

Форма каждого геометрического тела имеет свои характерные признаки. В основе формы деталей машин и механизмов также находятся геометрические тела. Чтобы понять по чертежу форму сложного предмета, его мысленно разделяют на части, представляющие собой геометрические тела, т. е. анализируют форму (рис. 8). Затем мысленно объединив эти части, воссоздают общую форму предмета.

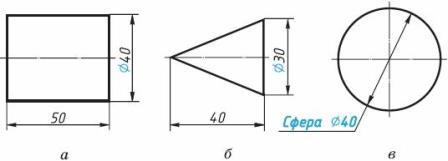
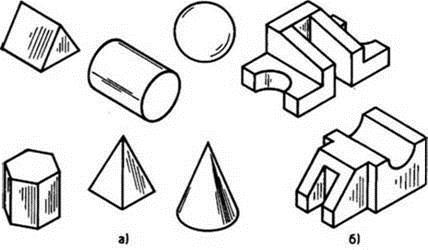
Рис. 8. Кофейник и его элементы

Геометрической формой называется внешний облик предмета, характеризующийся совокупностью его геометрических свойств. К геометрическим свойствам предметов относятся: раз­меры, пропорции, взаимное расположение составляющих элементов формы.

Предметы бывают простой и сложной формы. К предметам простой формы относятся те, которые представляют собой гео­метрические тела: цилиндр, конус, шар, призма, пирамида (рис. 9, а). К предметам сложной (составной) формы относятся такие, которые образованы сочетанием различных геометриче­ских тел (рис. 9, б).

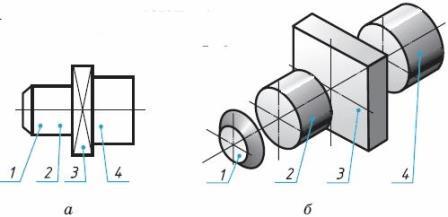
Рис. 9. Предметы простой (а) и сложной (б) формы

Основные геометрические тела можно выявить в любой детали или предмете. Так, на рисунке 10, а в прямоугольной проекции изображена деталь, называемая валиком (от слова «вал»). В ней можно выделить такие геометрические тела, как усеченный конус 1, цилиндр 2, параллелепипед 3 и еще один цилиндр, большего диаметра – 4 (рис. 10, б).

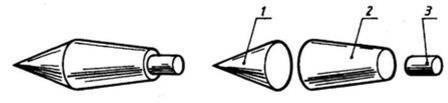
Рис. 10. Анализ геометрической формы детали

Чтобы представить по чертежу общую форму любой детали, необходимо выявить форму всех ее элементов. Для этой цели сложную по форме деталь мысленно разделяют на отдельные конструктивные части, имеющие форму различных геометрических тел. Мысленное разделение предмета на основные геометрические тела называют анализом геометрической формы предмета. Используя изображение детали, размерные числа, условные знаки и надписи, можно воссоздать образ детали, т. е. представить по чертежу ее пространственную форму.

Ещё проанализируем форму детали (рис. 11), состоящей из трех геометрических тел: конусов (прямого кругового и усеченного) и цилиндра.

Рис. 11. Анализ геометрической формы детали «Конус» на основе рас­членения ее на геометрические тела: 1 – конус; 2 – усеченный конус; 3 – цилиндр

 Все части, составляющие форму рассматриваемого изделия, расположены на одной оси (т. е. соосны). К основанию конуса примыкает равновеликое основание усеченного конуса. Другое основание усеченного конуса совмещается с основанием цилиндра, диаметр которого меньше диаметра конуса.

Попробуйте выполнить чертеж детали, представленной на рисунке 12.

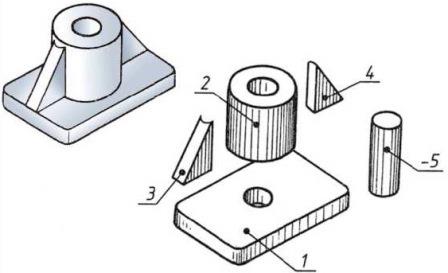
Рис. 12. Геометрическая разборка формы детали

Практические задания, тесты и домашние работы

Графическая работа

Вопросы для повторения

pdf 

Тест

Домашняя работа

pdf  Третий лишний

pdf  Отгадай форму

pdf  Согни бумагу по чертежу

pdf  Крыша дома

pdf  Чайники

pdf  В чём отличие?

pdf  Изобрази пробку

pdf  Модели из проволоки

pdf  Эвристическая задача