Приложения 

Ботвинников А.Д. § 15.3 [1]

pdf  Презентация "Сопряжение"

pdf  Презентация "Построение внешней касательной к двум окружностям"

pdf 

Лекальные кривые

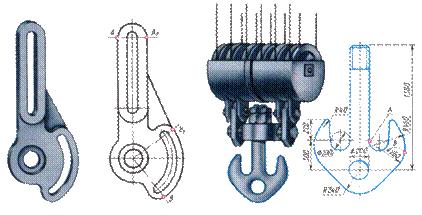
При вычерчивании деталей машин и приборов, контуры очертаний которых состоят из прямых линий и дуг окружностей с плавными переходами от одной линии в другую, часто применяют сопряжения (рис.1).

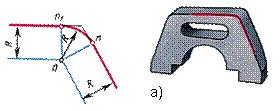
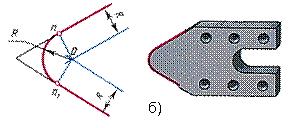
Сопряжением называется плавный переход одной линии в другую.

Для построения сопряжения надо найти:

Сопряжения бывают нескольких видов:

1) сопряжение двух прямых, расположенных:

2) сопряжение прямой и дуги:

Сопряжение двух прямых, расположенных под прямым углом дугой окружности заданного радиуса.

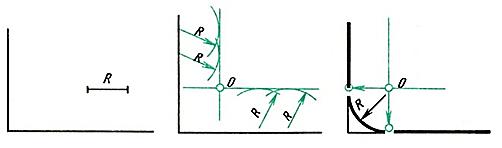
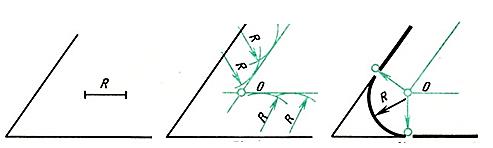
Рис. 2

а)сопряжение сторон острого угла; б) сопряжение сторон тупого угла.

Для всех трех случаев применяют общий способ построения.

1. Находят точку О - центр сопряжения, который должен лежать на расстоянии R от сторон угла в точке пересечения прямых, проходящих параллельно сторонам угла на расстоянии >R от них (рис. 3, 4, 5). Для построения прямых, параллельных сторонам угла, из произвольных точек, взятых на прямых, раствором циркуля, равным R, делают засечки и к ним проводят касательные.

Рис. 4. Сопряжение острого угла

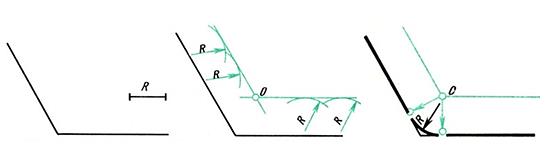
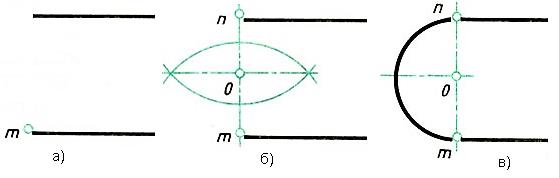
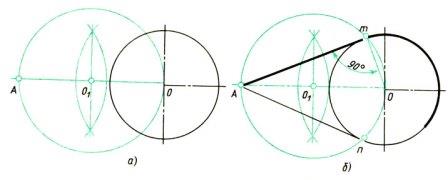
Рис.5. Сопряжение тупого угла

Сопряжение двух параллельных прямых

Заданы две параллельные прямые и на одной из них точка сопряжения m (рис. 6,а). Требуется построить сопряжение.

Построение выполняют следующим образом:

1. Находят центр сопряжения и радиус дуги (рис. 6,б). Для этого из точки m на одной прямой проводят перпендикуляр до пересечения с другой прямой в точке n. Отрезок делят пополам (см. здесь).

2. Из точки О - центра сопряжения радиусом Оm = Оn описывают дугу до точек сопряжения m и n (рис. 6, в).

Рис.6. Сопряжение двух параллельных прямых

Сопряжения прямой с дугой окружности

Проведение касательной к окружности от точки, принадлежащей окружности

Если задана окружность и надо построить касательную к этой окружности в заданной точке, то строят перпендикуляр к прямой, проходящий через центр окружности и заданную точку (рис.7).

Рис. 7

Проведение касательной к окружности от точки, не принадлежащей окружности

1. Точку А соединяют прямой с заданным центром О окружности.

Строят вспомогательную окружность диаметром, равным О₁А (рис. 8, а). Чтобы найти центр О₁ - делят отрезок ОА пополам (см. здесь).

2. Точки m и n пересечения вспомогательной окружности с заданной - искомые точки касания. Точку А соединяют прямой с точками m или n (рис. 8, б). Прямая Am будет перпендикулярна к прямой Оm, так как угол АmО опирается на диаметр.

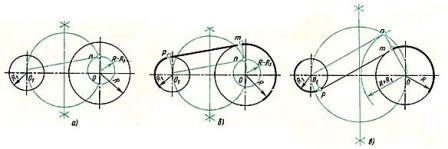
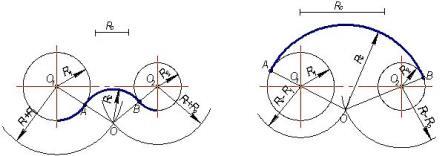
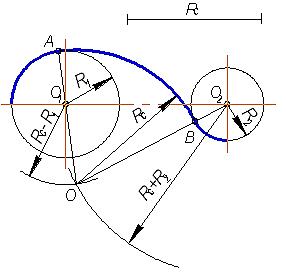
Рис. 8. Построение касательной к окружности

Проведение прямой, касательной к двум окружностям

Заданы две окружности радиусом R и R₁. Требуется построить касательную к ним.

Различают два случая касания: внешнее (рис. 9,б) и внутреннее (рис. 9, в).

При внешнем касании построение выполняют следующим образом:

1. Из центра О проводят вспомогательную окружность радиусом, равным разности радиусов заданных окружностей, т. е. R - R₁ (рис. 9, а). К этой окружности из центра О₁ проводят касательную Оm. Построение касательной показано на рис. 8.

2. Радиус, проведенный из точки О в точку n, продолжают до пересечения в точке m с заданной окружностью радиусом R. Параллельно радиусу Оm проводят радиус 0₁р меньшей окружности. Прямая, соединяющая точки сопряжений m и р,- касательная к заданным окружностям (рис. 9, б).

При внутреннем касании построение проводят аналогично, но вспомогательную окружность проводят радиусом, равным сумме радиусов R + R₁ (см. рис. 9, в). Затем из центра O₁проводят касательную к вспомогательной окружности (см. рис. 8). Точку n соединяют радиусом с центром О. Параллельно радиусу On проводят радиус O₁р меньшей окружности. Искомая касательная проходит через точки сопряжений m и р.

Рис. 9. Построение касательной к двум окружностям

Сопряжение дуги и прямой линии дугой заданного радиуса

Заданы дуга окружности радиусом R и прямая. Требуется соединить их дугой радиусом R₁.

1. Находят центр сопряжения (рис. 10,а), который должен находиться на расстоянии R₁ от дуги и от прямой. Такому условию соответствует точка пересечения прямой линии, параллельной заданной прямой, проходящей от нее на расстоянии R₁, и вспомогательной дуги, отстоящей от заданной также на расстоянии R₁. Поэтому проводят вспомогательную прямую, параллельную заданной прямой, на расстоянии, равном радиусу сопрягающей дуги R₁ (рис. 10, а). Раствором циркуля, равным сумме заданных радиусов R + R₁, описывают из центра О дугу до пересечения с вспомогательной прямой. Полученная точка O₁ - центр сопряжения.

2. По общему правилу находят точки сопряжения (рис. 10, б). Соединяют прямой центры сопрягаемых дуг O₁ и О. Опускают из центра сопряжения O₁ перпендикуляр на заданную прямую.

3. Из центра сопряжения O₁ между точками сопряжения m и n проводят дугу, радиус которой равен R₁ (см. рис. 10, б).

Рис. 10. Сопряжение дуги окружности и прямой

Сопряжение двух дуг окружности дугой заданного радиуса

Заданы две дуги радиусами R₁ и R₂. Требуется построить сопряжение дугой, радиус которой задан.

Различают три случая касания: внешнее, внутреннее и смешанное.

При внешнем сопряжении центры О₁ и О₂ сопрягаемых дуг радиусов R₁ и R₂ находятся вне сопрягающей дуги радиуса R (рис. 11, а).

При внутреннем сопряжении центры О₁ и О₂ сопрягаемых дуг находятся внутри сопрягающей дуги радиуса R(рис. 11, б).

При смешанном сопряжении центр О₁ одной из сопрягаемых дуг лежит внутри сопрягающей дуги радиуса R, а центр О₂ другой сопрягаемой дуги вне ее (рис.13).

Во всех случаях центры сопряжений должны быть расположены на расстоянии, равном радиусу дуги сопряжения, от заданных дуг. По общему правилу на прямых, соединяющих центры сопрягаемых дуг, находят точки сопряжения.

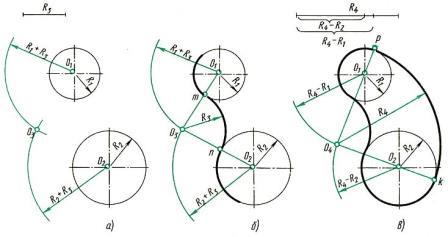
Рис. 11. Сопряжение дуг окружностей

а) внешнее сопряжение;    б) внутреннее сопряжение

Ниже приведен порядок построения для внешнего и внутреннего сопряжения.

Для внешнего сопряжения:

1. Из центров O₁ и О₂ раствором циркуля, равным сумме радиусов заданной и сопрягающей дуг, проводят вспомогательные дуги (рис. 12,а); радиус дуги, проведенной из центра O₁, равен R + R₃, а радиус дуги, проведенной из центра O₂, равен R₂ + R₃. На пересечении вспомогательных дуг расположен центр сопряжения - точка О₃,.

2. Соединив прямыми точку O₁ с точкой O₃ и точку O₂ с точкой O₃, находят точки сопряжения m и n (см. рис. 12, б),

3. Из точки О₃ раствором циркуля, равным R₃, между точками m и n описывают сопрягающую дугу.

Для внутреннего сопряжения выполняют те же построения, но радиусы дуг берут равными разности радиусов сопрягающей и заданной дуг, т.е. R₄ - R₁ и R₄ - R₂. Точки сопряжения р и k лежат на продолжении линий, соединяющих точку О₄ с точками O₁ и O₂.

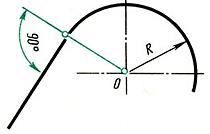
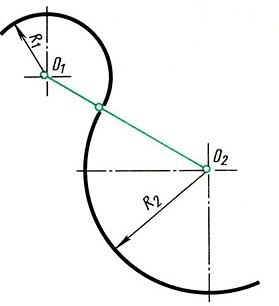
Рис. 12. Сопряжение двух дуг окружности

Заданы две дуги радиусами R₁ и R₂ с заданным расстоянием между центрами. Требуется построить сопряжение дугой, радиус которой задан.

По заданному расстоянию между центрами на чертеже намечают центры О₁ и О₂, из которых описывают сопрягаемые дуги радиусов R₁ и R₂. Из центра О₁ проводят вспомогательную дугу окружности радиусом, равным разности радиусов сопрягающей R и сопрягаемой дуги R₁, а из центра О₂ - радиусом, равным сумме радиусов R и R₂. Вспомогательные дуги пересекутся в точке О, которая будет искомым центром сопрягающей дуги.

Соединив точки О и О₁ прямой, находят точку сопряжения А; соединив точки О и О₂, получают точку сопряжения В. Из центра О проводят дугу сопряжения от А до В.

Рис. 13. Смешанное сопряжение

Для точного и правильного выполнения чертежей необходимо уметь выполнять построения сопряжений, которые основаны на двух положениях.

1. Для сопряжения прямой линии и дуги необходимо, чтобы центр окружности, которой принадлежит дуга, лежал на перпендикуляре к прямой, восставленном из точки сопряжения.

2. Для сопряжения двух дуг необходимо, чтобы центры окружностей, которым принадлежат дуги, лежали на прямой, проходящей через точку сопряжения.

При вычерчивании контура детали необходимо разобраться, где имеются плавные переходы, и представить себе, где надо выполнить те или иные виды сопряжения.

Для приобретения навыков построения сопряжения выполняют упражнения по вычерчиванию контуров сложных деталей. Перед упражнением необходимо просмотреть задание, наметить порядок построения сопряжений и только после этого приступить к выполнению построений.

Нахождение точек сопряжения показано на рисунке 14.

Рис. 14. Нахождение точек сопряжения

Пример сопряжения

Практические задания, тесты и домашние работы

Графическая работа  

Вопросы для повторения

Тест

Домашняя работа

pdf  Забавные животные

pdf  Кошечка

pdf  А вам слабо?

pdf