Приложения 

Ботвинников А.Д. § 15.2 [1]

Степакова В. В. § 15 [3]
Вышнепольский И.С. § 8 [8]


pdf  Проведение параллельных прямых

pdf  Деление отрезка на 2 равные части

pdf  Деление отрезка на равные части

pdf  Построение перпендикуляра к прямой

pdf  Деление углов на равные части

pdf  Построение углов с помощью циркуля

pdf  Нахождение центра дуги



pdf  Презентация "Деление окружности на равные части"

pdf 

При выполнении графических работ приходится решать многие задачи на построение. Наиболее встречающиеся при этом задачи — деление отрезков прямой, углов и окружностей на равные части, построение различных сопряжений.

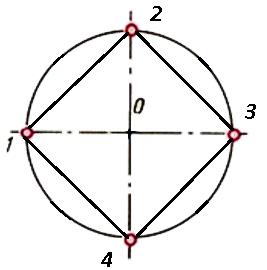
Деление окружности на равные части с помощью циркуля

Пользуясь радиусом, нетрудно разделить окружность и на 3, 5, 6, 7, 8, 12  равных участков.

Деление окружности на четыре равные части

Штрихпунктирные центровые линии, проведенные перпендикулярно одна другой, делят окружность на четыре равные части. Последовательно соединив их концы, получим правильный четырехугольник (рис. 1).

Рис.1 Деление окружности на 4 равные части.

Деление окружности на восемь равных частей

Чтобы разделить окружность на восемь равных частей, дуги, равные четвертой части окружности, делят пополам. Для этого из двух точек, ограничивающих четверть дуги, как из центров радиусов окружности выполняют засечки за ее пределами. Полученные точки соединяют с центром окружностей и на пересечении их с линией окружности получают точки, делящие четвертные участки пополам, т. е. получают восемь равных участков окружности (рис. 2).

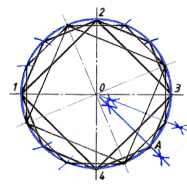
Рис.2. Деление окружности на 8 равных частей.

Деление окружности на шестнадцать равных частей

Разделив циркулем дугу, равную 1/8, на две равные части, нанесём засечки на окружность. Соединив все засечки, отрезками прямых, получим правильный шестнадцатиугольник.

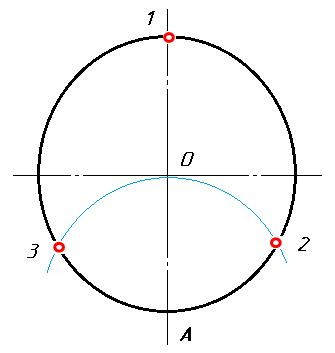
Рис.3. Деление окружности на 16 равных частей.

Деление окружности на три равные части

Чтобы разделить окружность радиуса R на 3 равные части, из точки пересечения центровой линии с окружностью (например, из точки А) описывают как из центра дополнительную дугу радиусом R. Получают точки 2 и 3. Точки 1, 2, 3 делят окружность на три равные части.

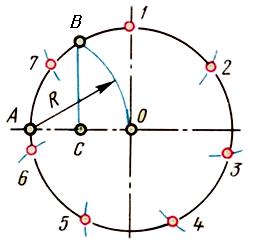
Рис. 4. Деление окружности на 3 равные части.

Деление окружности на шесть равных частей. Сторона правильного шестиугольника, вписанного в окружность, равна радиусу окружности (рис. 5.).

Для деления окружности на шесть равных частей надо из точек 1 и 4 пересечения центровой линии с окружностью сделать на окружности по две засечки радиусом R, равным радиусу окружности. Соединив полученные точки отрезками прямых, получим правильный шестиугольник.

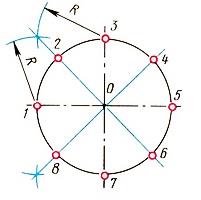
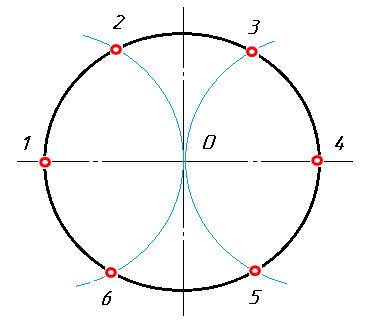
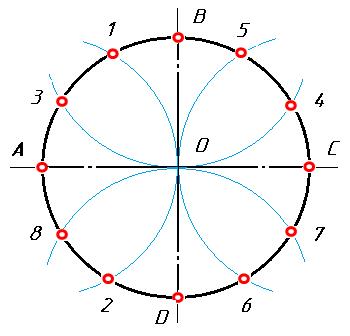
Рис. 5. Деление окружности на 6 равных частей

Деление окружности на двенадцать равных частей

Чтобы разделить окружность на двенадцать равных частей, надо окружность поделить на четыре части взаимно перпендикулярными диаметрами. Приняв точки пересечения диаметров с окружностью А, В, С, D за центры, величиной радиуса проводят четыре дуги до пересечения с окружностью. Полученные точки 1, 2, 3, 4, 5, 6, 7, 8 и точки А, В, С, D разделяют окружность на двенадцать равных частей (рис. 6).

Рис. 6. Деление окружности на 12 равных частей

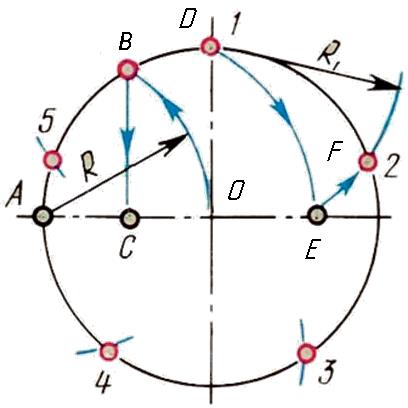
Деление окружности на пять равных частей

Из точки А проведем дугу тем же радиусом, что и радиус окружности до пересечения с окружностью – получим точку В. Опустив перпендикуляр с этой точки – получим точку С.   Из точки С – середины радиуса окружности, как из центра, дугой радиуса СD сделаем засечку на диаметре, получим точку Е. Отрезок DЕ равен длине стороны вписанного правильного пятиугольника. Сделав радиусом DЕ засечки на окружности, получим точки деления окружности на пять равных частей.

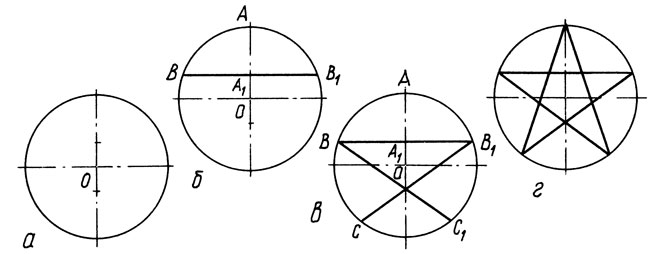
Рис. 7. Деление окружности на 5 равных частей

Другой вариант деления на 5 равных частей

Разметка по третьей части диаметра. Проводят окружность нужного размера, диаметр делят на три части (рис. 8, а). Через точку А₁ проводят линию, параллельную горизонтальному диаметру (рис. 8, б). Из точек В, В₁ проводят линии через вторую засечку на вертикальном диаметре (рис. 8, в). Соединяют точку А с точками С, С₁. Звездочка готова (рис. 8, г).

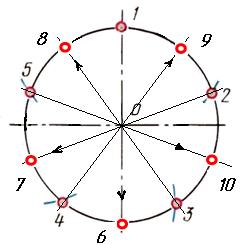
Рис. 8. Деление окружности на 5 равных частей

 Деление окружности на десять равных частей

Разделив окружность на пять равных частей, легко можно разделить окружность и на 10 равных частей. Проведя прямые от получившихся точек через центр окружности до противоположных сторон окружности – получим ещё 5 точек.

Рис. 9. Деление окружности на 10 равных частей

Деление окружности на семь равных частей

Чтобы разделить окружность радиуса R на 7 равных частей, из точки пересечения центровой линии с окружностью (например, из точки А) описывают как из центра дополнительную дугу этим же радиусом R – получают точку В.  Опустив перпендикуляр с точки В – получим точку С.   Отрезок ВС равен длине стороны вписанного правильного семиугольника.

Рис. 10. Деление окружности на 7 равных частей

Практические задания, тесты и домашние работы

Графическая работа

Вопросы для повторения

pdf  Вопросы

Тест

Домашняя работа

pdf  Пятиугольники